▶소프트웨어 개발 과정
- (도메인 분석) → 계획 → (요구)분석 → 설계 → 구현 → 테스트 → 유지보수
- 소프트웨어를 만들기 위해 계획 단계에서 유지보수 단계까지 이르기까지 일어나는 일련의 과정
- 소프트웨어 개발 생명주기라고 함
▶ 1단계: 계획
- 비용, 기간 등 프로젝트를 수행하는 데 필요한 것에 대해 계획함
- 계획 단계에서 비용을 산정하는 대표적인 방법으로 COCOMO 모델, 기능 점수(FP, Function Point)모델 존재
- 계획 단계에서는 일정 계획이 매우 중요
- 프로젝트를 작은 단위로 나누어 작업할 수 있도록 하는 작업 분할 구조도(WBS) 존재
- 작업의 순서와 시간을 중심으로 작업 일정을 나타내는 네트워크 차트(CPM) 존재
- 프로젝트를 수행할 때 어떤 위험이 존재하는지 파악하고 이를 예방할 수 있는 조치를 취해야함
▷계획 단계의 주요 작업: 문제 정의, 타당성 분석, 예산 계획, 일정 계획, 위험 분석, 계획서 작성
▶ 일정 계획
- 소프트웨어를 개발하기 위해 어떤 작업이 필요한지 찾은 후, 이를 진행할 순서를 결정하거나 주어진 개발 기간에 소작업의 개발 기간 및 그들 간의 순서, 필요한 자원 등과 같은 일정을 계획하는 것
ex) 대학의 종합정보시스템에서 학사 관리 어플리케이션 일정 계획

▷일정 계획의 시작 :WBS(Work Breakdown Structure),
- 프로젝트 목표를 달성하기 위해 필요한 활동과 업무를 세분화하는 작업
- 프로젝트 구성 요소들을 계층 구조로 분류하여 프로젝트의 전체 범위를 정의하고, 프로젝트 작업을 관리하기 쉽도록 세분화함
- 이때 계층 구조에서 최하위에 있는 항목을 작업 패키지라고 하며, 작업 패키지는 해당 업무의 담장자를 할당할 수 있을 정도로 작게 나눔
● 학사 관리 시스템 WBS

● WBS의 목적 및 용도
- 사용자와 개발자 간의 의사소통 도구로 사용함
- 프로젝트 업무 내역을 가시화할 수 있어 관리 용이함
- 프로젝트 팀원의 책임과 역할이 분명함
- 필요 인력과 일정 계획을 세우는 기초로 활용함
- 개발비 산정 시 기초로 활용함
- 성과 측정 및 조정 시 기준선으로 활용할 수 있음
▷일정 계획
네트워크 차트(PERT/CPM)
- WBS의 작업 순서, 소요 기간 등을 네트워크 형태의 그래프로 표현한 후 완료일에 프로젝트를 마치려면 어떤 작업이 중요한지, 또 일정에 여유가 있는 작업은 어떤 것인지 찾아내 중점 관리를 해야 하는 작업을 명확히 하는데 사용
- 프로젝트를 완료할 수 있는 최소 기간은 얼마인지, 완료 기간을 맞추기 위해서는 각 작업을 언제 시작하고 완료해야 하는지, 지연되지 않으려면 어떤 작업에 특히 주의를 기울여야 하는지, 또 전체 프로젝트 완료 기간을 단축하기 위해서는 어떤 작업들을 단축하는 것이 가장 경제적인지 등 관리자의 고민에 답을 주기 위해 필요한 도구
● PERT
- 프로그램을 평가하고, 검토하는 프로젝트 관리 기법
- 프로젝트 진행 상황을 통계적인 방법으로 파악하고 이를 통해 일정 계획 및 통제를 할 수 있도록 고안됨
● CPM
- 미 듀퐁사에서 화학 처리 공장의 건설 계획을 조직적으로 추진하기위해 개발됨
- 건설 공사와 같이 단위 작업이 확정적 소요 시간을 갖는 프로젝트에 적합함
- PERT와 CPM은 비슷한 형태를 띠고 있으면서도 다름
- 이러한 유사성과 상호 장단점 때문에 PERT/CPM이라 하여 두 기법을 혼합한 방법을 사용하기도 함
- CPM으로 네트워크를 그리려면 다음 [표 1]와 같이 학사 관리 애플리케이션을 수행하는 데 필요한 작업, 선행 작업, 작업의 소요 기간을 알아야함.
● CPM 네트워크를 위한 활동 목록
(CPM 네트워크에 대한 이해를 돕기 위해 작성한 예로, 선행 작업의 순서는 실제와 다름)

① CPM 네트워크를 그린다
- 노드(node)와 간선(edge)을 이용해 [표 1]에 대한 초기의 CPM 네트워크를 [그림 1]와 같이 그린다.
- 노드는 작업을, 간선은 작업들 간의 선후 의존관계를 나타낸다. 즉 화살표 뒤의 작업은 화살표 전의 작업이 끝나야 시작할 수 있다.
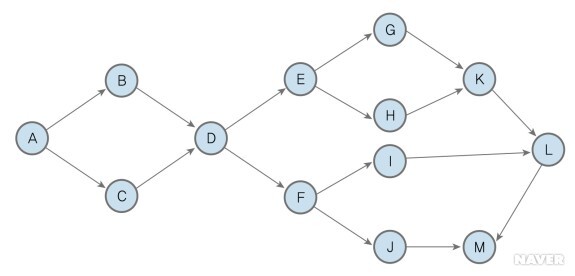
② ES 값을 구한다
- ES(Earliest Start time)는 가능한 빨리 시작할 수 있는 시간으로, 선행 작업이 완료되었을 때 해당 작업을 시작할 수 있는 가장 빠른 시점이다.
ES 값을 구할 때는 맨 앞(작업 A)에서 끝 방향으로 가며 계산한다. 작업 A는 시작 시간으로서 0이고, 작업 B는 작업 시간이 2인 작업 A가 끝나야 하므로 2가 된다. 작업 C도 2가 된다. 그런데 작업 D는 작업 시간이 2인 작업 A와 작업 시간이 6인 B도 끝나고(A-B), 작업 시간 2인 작업 A와 작업 시간 4인 작업 C도 끝나야(A-C) 시작할 수 있다. 그러므로 작업 D를 시작할 수 있는 조건은 경로 1(A-B)과 경로 2(A-C)를 모두 마치는 것이므로 가장 빨리 시작할 수 있는 값은 경로 1(A-B-D, 시작 시간 8)과 경로 2(A-C-D, 시작 시간 6)를 모두 만족시키는 8이 된다.
같은 방법으로 작업 E~J는 각각 10, 10, 14, 14, 13, 13이 된다. 그런데 작업 K는 16, 18 두 개의 값이 나온다. 무엇을 선택해야 할까? 작업 D처럼 큰 값을 선택해야 앞의 두 경로(G-K, H-K)를 만족시킬 수 있다. 또 작업 L도 작업 K와 I의 합류 지점으로, 두 경로(K-L, I-L)의 값 20과 15 중 큰 값을 선택해야 한다. 작업 M도 합류 지점으로 큰 값을 선택하면 22가 된다. 이를 정리하면 [표 2]과 같다.
ES에서 주의할 부분은 두 작업이 합류하는 지점이다. 즉 작업 D, K, L, M이다. 이 작업의 시작 시간은 두 작업이 모두 완전히 끝났을 때를 시작 시간으로 보면 된다.
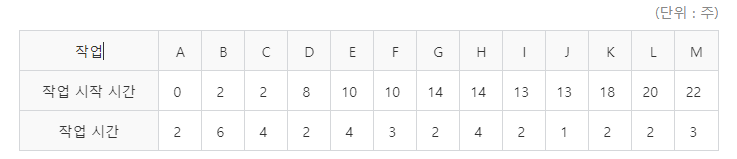
③ EF 값을 구한다
EF(Earliest Finish time)는 가장 빠른 시작 시간(ES)으로 시작했을 때의 가장 빠른 완료 시간이다. 즉 가능한 빨리 끝낼 수 있는 시간으로 'ES+작업 소요 시간'이다.
예를 들면, D 작업은 가장 빠른 시작 시간이 8이고 작업 소요 시간이 2이므로 가장 빨리 끝날 수 있는 시간은 10이다. 마찬가지로 K 작업은 가장 빠른 시작 시간이 18이고 작업 소요 시간이 2이므로 가장 빨리 끝날 수 있는 시간은 20이다. 모든 작업에서 가장 빨리 완료할 수 있는 시간은 [표 3]와 같다.

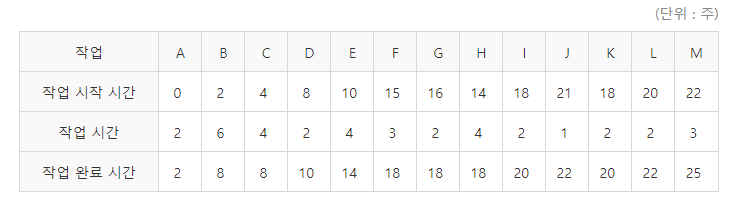
④ LS 값을 구한다
LS(Latest Start time)는 어떤 작업을 늦어도 시작해야 하는 시간, 즉 가장 늦게 시작할 수 있는 시간을 말한다. 이 시간에 시작하지 않으면(이 시간보다 늦게 시작하면) 총 일정이 지연된다. 값을 구하는 방법은 ES와 EF가 맨 앞에서부터 계산했다면 LS는 맨 뒤(작업 M)에서 앞(작업 A) 방향으로 계산한다.
마지막 작업인 M을 22에는 시작(그보다 나중에 시작하면 전체 일정이 그만큼 늦어진다)해야 하므로 작업 시간이 2인 작업 L이 20에는 시작해야 작업 M을 차질 없이 22에 시작할 수 있다. 마찬가지로 작업 시간이 1인 작업 J도 M의 시작 시간(22)에 맞추려면 21에 시작하면 된다. 또 작업 L의 시작 시간이 20이므로 작업 시간이 2인 작업 K는 18에, 작업 시간이 2인 작업 I도 18에는 시작해야 된다.
작업 K를 18에 시작하므로 작업 시간 2인 작업 G는 16에, 작업 시간 4인 작업 H는 14에 시작하면 작업 G와 H의 후속인 작업 K를 시작하는 데 문제가 없다. 그런데 작업 시간 3인 작업 F는 시작 시간이 18인 작업 I에도 맞춰야 하고, 시작 시간이 21인 작업 J에도 맞춰야 한다. 작업 I에만 맞추면 시작 시간은 15가 되고, 작업 J에만 맞추면 19가 된다. 15에 맞춰야 할까, 아니면 19에 맞춰야 할까? 19에 맞추면 작업 J의 시작 시간에는 영향을 미치지 않지만, 시작 시간이 18인 작업 I에는 큰 영향을 준다. 따라서 15에 맞춰야 작업 I와 J 모두에 영향을 주지 않는다.
마찬가지로 작업 E도 작업 G에 맞추면 12, 작업 H에 맞추면 10이 된다. 둘 다 영향을 주지 않는 것은 10이다. 이와 같은 방법을 반복하면 작업 D는 8, 작업 C는 4, 작업 B는 2, 작업 A는 0이 되어 [표 4]과 같이 된다.
LS에서도 주의할 부분은 두 지점으로 갈라지는 곳으로 F, E, D, A가 이에 해당된다. 예를 들어, D 작업은 경로 1(A-B)과 경로 2(A-C)가 모두 끝나야 시작할 수 있다. 경로 2(6)가 먼저 끝났다고 해서 경로 1(8)이 안 끝났는데 시작할 수는 없다. 그러므로 경로 2(A-C)는 조금 천천히 작업해도 D 작업을 시작하는 데 영향을 주지 않는다. 그럼 얼마나 천천히 할 수 있을까? 2주의 여유가 있다. 경로 1이 끝나기 전까지 끝내거나 경로 1과 동시에 끝내도 된다. 이처럼 다음 작업 D의 시작 시간에 영향을 주지 않고 시작할 수 있는 시간을 찾아 적어주면 된다. 그래서 정리하면 [표 4]과 같다.

⑤ LF 값을 구한다
LF(LatestFinishtime)는 가장 늦게 시작할 수 있는 시간(LS)에 시작해 작업을 완료한 시간을 말한다. 즉 작업을 가장 늦게 끝낼 수 있는 시간으로 'LS+작업 소요 시간'이다. 정리하면 [표 5]과 같다.
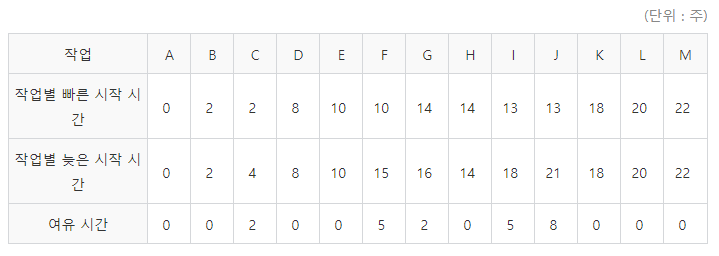
⑥ ST 값을 구한다
ST(Slack Time)에서 Slack의 사전적 의미는 '느슨한', '여유 있는'이므로 Slack Time은 '느슨한 시간', '여유 있는 시간'이다. 그럼 작업에서 느슨하게, 여유 있게 할 수 있는 시간이 과연 있을까? 있다.
예를 들어, 두 팀이 서로 다른 등산로로 등산하는데(같은 곳에서 7시에 동시 출발) 중간에 특정 두 지점 A, B를 정해놓은 후, A 지점에서는 간식을 함께 먹고 동시에 9시에 출발하고, B 지점에서는 11시에 만나 함께 점심을 먹고 1시에 출발하기로 했다. 이때 각 지점에 한 팀이 30분 일찍 도착한다면 그만큼의 시간 여유가 생긴다. 또는 한 팀의 등산로 코스가 쉽고 짧은 경우 주변 경치를 즐기며 천천히 등산해도 만나는 지점에 제때 도착할 수 있을 것이다.
이처럼 작업에도 여유 시간이 존재한다. [그림 1]에서 작업 D까지 도달하는 데 경로 1(A-B-D)은 8, 경로 2(A-C-D)는 6으로, 경로 2는 2주간의 여유 시간이 생긴다. 이처럼 곳곳에 존재하는 여유 시간을 찾는 일이 매우 중요하다. 전체 작업 시간을 줄이고 싶을 때는 여유 시간이 존재하는 작업의 시간을 줄이면 된다.
그럼 여유 시간을 구하는 방법을 알아보자. 여유 시간은 각 작업에서 '가장 늦게 시작하는 시간'에서 '가장 빨리 시작하는 시간'을 빼면 되는데 결과는 [표 6]와 같다.
⑦ 임계 경로를 구한다
- 임계 경로: 여러 단계의 과정을 거치는 작업에서 그것을 완성하려면 여러 과정의 경로가 동시에 수행되어야 한다고 할 때, 그중 가장 긴 경로. 즉, 전체 공정 중 시간이 가장 많이 걸리는 경로
- 임계 경로(critical path)는 [그림 2] 의 그래프에서 여유 시간이 없는 경로를 말한다. 여기서는 경로 'A-B-D-E-H-K-L-M'이 임계 경로가 된다. 임계 경로에는 여유 시간이 없으므로 모든 일정 계획은 임계 경로에 좌우된다.
임계 경로에 있는 작업 하나가 1일 지연되면 전체 일정도 똑같이 1일 지연된다. 반대로 전체 프로젝트 완료 시간을 단축하고 싶다면 임계 경로의 작업 시간을 줄이면 된다.
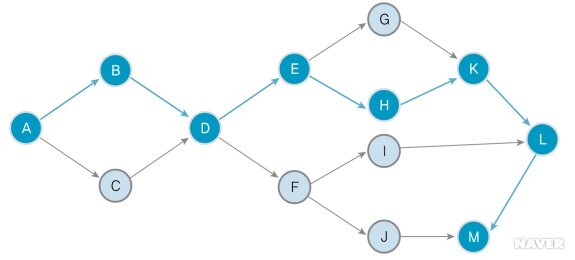
한편, 임계 경로에서 벗어난 활동을 수행하는 데 걸리는 시간이 한도 내에서 늦춰지거나 당겨질 경우에는 전체 프로젝트 완료 시간에 변화가 없다. 예를 들어 작업 I가 2주 지연되더라도 5주의 여유 시간이 있어(임계 경로에 없음) 프로젝트의 최종 완료일에 영향을 주지 않는다.
실제 프로젝트에서는 초기에 세운 일정 계획대로 진행되지 않는다. 프로젝트가 진행됨에 따라 계획과 비교하여 그 결과를 후반 일정을 수정하는 데 사용하며 네트워크 차트도 다시 그린다. 그러므로 이때 전체 일정을 늦추지 않으려면 임계 경로 상의 작업 시간을 줄이기 위해 재구성해야 할 것이다.
▷일정 계획 기법2 :간트 차트
- 간트 차트는 프로젝트 일정 관리를 위한 바(bar)형태의 도구
- 프로젝트의 주요 활동을 파악한 후, 각 활동의 일정을 시작하는 시점과 끝나는 시점을 연결한 막대 모양으로 표시하여 전체 일정을 한눈에 볼 수 있게함

▶ 위험 관리·분석
- 위험 관리는 소프트웨어 개발에 방해가 되는 요소를 파악하고(위험 요소 식별),
- 위험 요소의 발생 확률과 영향도를 평가한 뒤(위험분석),
- 분석한 결과에 따라 위험 우선순위를 정하여 그에 맞게 대책을 세우는 것

① 위험 요소 식별
- 위험 관리에서 가장 중요한 일은 프로젝트 수행에 영향을 주는 위험 요소를 파악하는 것
- 위험 요소를 찾는 방법에는 팀원들이 모여 발생 가능한 위험 요소에 대해 브레인스토밍하여 도출하는 방법 존재
- 이전에 유사한 프로젝트를 진행할 때 발생한 위험 요소를 참조하는 방법 존재
- 찾은 위험 요소의 원인을 규명하는 일도 해결책을 강구하는데 중요
● 프로젝트 수행 시 발생할 수 있는 위험 요소

② 위험 분석
- 위험 요소를 식별했다면 그 위험 요소가 발생할 가능성과 영향력을 판단해야 함
- 위험 발생 가능성의 척도는 매우 낮음, 낮음, 보통, 높음, 매우 높음과 같은 등급으로 분류할 수 있음
- 위험 영향력은 재앙, 심각함, 해결 가능함, 경미함 등으로 분류할 수 있음
- 위험 영향력은 비용과 일정이 20% 이상 초과하면 상, 5~20%이면 중, 5%이하이면 하로 분류할 수 있음
- 도출된 위험 요소에 대한 가능성과 영향력을 등급으로 나타냈다면 이를 이용해 어떤 위험이 가장 중요하지 순위를 정함
③ 위험 계획 수립
- 식별된 위험 요소의 위험을 관리하기 위해 전략을 찾는 과정
- 이 과정에서는 위험을 처리하는 대응 방안을 잘 세워야함
ex) 요구 사항이 계속 변경되면 고객과 그 문제를 재협의할 수도 있고, 고객 입장에서 개발비가 많다고 하면 금년의 개발 범위를 줄이고 연차적으로 개발하는 방법을 제시할 수도 있음
④ 위험 감시
- 위험 요소가 식별되었다고 문제가 해결되진 않음
- 식별된 위험은 계속 감시해야함
- 식별된 위험 요소의 발생 확률과 변화 등을 관리해야 함
- 프로젝트가 종료되면 시작 시 예측된 위험 요소가 실제로 얼마나 발생했는지, 위험에 대한 대응 방안이 실제 발생했을 때 적절했는지 등을 평가하고, 앞으로 유사한 프로젝트를 진행할 때 참고할 수 있도록 개발사 내의 데이터베이스에 기록해놓아야 함
쉽게 배우는 소프트웨어 공학, 2015. 11. 30., 김치수
'[SW 공학]' 카테고리의 다른 글
| [SW 공학] 설계 (0) | 2023.10.11 |
|---|---|
| [SW 공학] 요구 분석 (1) | 2023.10.11 |
| [SW 공학] 계획-1 (1) | 2023.09.25 |
| [SW 공학] 개요 (0) | 2023.09.24 |




댓글